PS5 Vs Xbox. Price!

El año 2020 va a estar marcado por cientos de eventos que se engloban entre lo terrorífico y la crisis existencial. Saldrán, además, nuevas consolas. Sony con su PlayStation5 y Microsoft con su XBox Series X que parecen querer dejarnos para final de año un pequeño regalito que nos quite este mal sabor de boca que nos está dejando un universo enfurecido.
Conocemos el diseño de ambas consolas, ciertos elementos técnicos e incluso algunos de los juegos que podremos disfrutar durante estas primeras navidades con olor a generación 4K. Pero no sabemos el precio. Lo intuimos. Lo tememos. Nos empieza a doler la cartera. Alguna hucha que otra ya se ha empezado a llenar. Pero la incertidumbre sobre el precio sigue estando presente. Demasiadas variables y demasiado en juego parecen estar forzando a las compañías a retrasar la decisión sobre un número de 3 cifras que conoceremos en los próximos meses.
A todo esto viene el conocido juego del ratón y el gato. Sony está esperando a Microsoft. Y Microsoft está esperando a Sony. Pero, ¿Por qué?
Como muchas cosas en esta vida la explicación es bastante sencilla pero, como economista que soy, me voy a encargar en este artículo de rodearla de palabraría y un modelito matemático que nos permita hacer algo más serio ese “análisis” de por qué es mejor esperar a decidir el precio.
La información es poder. No es difícil entender por tanto que es mejor decidir con información en la mano que sin ella. Conocer el precio que va a poner tu competidor te deja en bandeja el intentar superarle. Y esperar a que tu competidor muestre sus cartas suele ser una estrategia nada desdeñable. Dicho grosso modo, la empresa X está esperando a que la empresa Y diga su precio para poder poner uno más barato (o para no pasarse de largo) e intentar robar una parte del pastel que le sería más difícil conseguir si ambas tuvieran que decidir y decir el precio con los ojos vendados.
Es curioso, no obstante, que el que elija segundo sea el que salga ganando en este duelo, sobre todo cuando casi todo estudiante de economía acaba sus estudios microeconómicos viendo el modelo de Stackelberg, un modelo en donde el que elije primero, obtiene más beneficio. La diferencia, como siempre es importante recalcar, es que los modelos son abstracciones que se nutren de unas hipótesis iniciales. Si estas no se cumplen, el modelo no nos vale para describir la microrealidad que estamos estudiando. En este caso el modelo de Stackelberg se refiere a la competencia empresarial en cantidades de un producto homogéneo. Esto es: Ambas empresas hacen un producto similar que compartirán el mismo precio en un mercado en dónde los consumidores no distinguen entre empresas. En este contexto, la primera empresa que consiga “copar” el mercado se va a llevar el gato al agua.
La realidad es que la competencia entre Sony y Microsoft se parecen a esos modelos iniciales como un huevo a una castaña. La diferencia fundamental es que ambas empresas están diferenciadas, en mayor o menor grado, y eso implica que aunque exista una cierta sustituibilidad entre los productos que vendan una y otra, no son exactamente iguales. Esa diferenciación implica que cada empresa debe elegir un precio y dejar que los consumidores decidan en base a ese precio cuantas unidades específicas de los productos de esa empresa comprar.
¿Cómo podemos crear un modelo que recoja esta competencia oligopolística (entre dos empresas) con un producto diferenciado que va a competir en precios? Como todo modelo, nos vamos a dejar muchas cosas por el camino, pero intentaremos destacar lo más importante.
Primero, vamos a utilizar unas funciones de demanda con las que he trabajado bastante que son las de Dixit-Stiglitz. Éstas se basan en el concepto de “competencia monopolística”, en donde se intenta unir el hecho de que empresas diferentes con marcas específicas (y por tanto con el monopolio de la identidad de su producto) compiten por satisfacer necesidades concretas o similares (con cierto grado de sustituibilidad entre los productos).
Supondremos que existen dos empresas (empresa 1 y empresa 2). La cantidad de demanda (q) de cada una de las empresas se puede describir de la siguiente manera:
Lo primero que voy a quitarme de en medio para hacer un poco más simple el análisis es el valor de sigma. Este parámetro mide precisamente el grado de diferenciación del producto. Va desde 1 hasta infinito. Es el valor de la elasticidad de demanda o del grado de homogeneidad del producto.
Si el valor fuera muy alto, significaría que el producto es muy elástico y homogéneo, es decir, un consumidor que tenga que elegir entre las dos empresas elegirá siempre el producto más barato porque, por lo demás, le parecen idénticos.
Si el valor fuera muy bajo, el producto sería menos elástico y, por tanto, más diferenciado. En este caso que una empresa suba el precio va a hacerle perder clientes, pero no muchos, porque tiene una gran parte del mercado que “va a caer al pozo” y comprar su producto siempre y cuando el precio no se vaya de madre. Su producto es tan diferenciado que el que tu producto pueda ser más caro no va a hacer directamente que los clientes salten a comprar los productos de la competencia.
Por descontado, las empresas no solo eligen cuánto producir y a qué precio poner sus productos en las tiendas. La variable de la diferenciación es crucial para crear ese mercado menos elástico sobre el que poder poner unos precios más altos. En el tema que nos toca, las videoconsolas, dos claros ejemplos me vienen a la mente: La potencia y los exclusivos. Pueden diferenciarse intentando meterle más teraflops (la variable de moda en esta entrada a la nueva generación) y además Sony y Microsoft disponen de estudios propios y externos que hacen juegos específicos para sus consolas. En este contexto, comprar la más barata ya no es lo más importante, si lo que quieres es jugar a Bloodborne 2 o al nuevo Halo.
En lo que concierne al modelo, vamos a suponer para hacer las cuentas más simples que el valor es de 2. De esta forma los exponentes quedan más sencillos (después relajaré un poco este supuesto para que podamos ver algunas extensiones interesantes). En cualquier caso, por si a alguno le interesa, la conclusión más importante del parámetro $\sigma$ es que, contra más bajo sea, mayor poder monopolístico tendrán las empresas (más importante será el concepto de marca) y mayor serán los precios y los beneficios. Hasta Desatranques Jaen conoce bien el poder de la diferenciación del producto.
La otra parte que nos queda ($\mu \cdot Y$) hace referencia al dinero que la gente se va a gastar en videoconsolas. Contra mayor sea la renta de la gente($Y$), o mayor sea el % de su gasto que quieran destinar a gastar en videoconsolas ($\mu$, que como es un “bien de lujo” crecerá también conforme crezca la renta), más consolas venderán. Algo bastante obvio que luego realmente no va afectar al precio óptimo.
Vale. ¿Qué hace una empresa para optimizar su producto? Coge su función de beneficio y la optimiza. Si el producto es homogéneo, el precio va a venir determinado por un mercado al que el producto de cada empresa le es indiferente, y lo que la empresa puede decidir es cuánta cantidad quiere producir y enviar al mercado. Si es diferenciado, como en este caso, la empresa tiene un cierto poder de decisión sobre su precio, permitiéndose poner un precio particular a su producto. Supondremos, pues es el origen del análisis de este artículo, que la empresa elije el precio que maximiza su beneficio.
¿Cuál es su beneficio?
Pues ingresos menos costes, claro. Ah, pero para el carro que la cosa no es tan simple. Obviamente la empresa incurrirá en unos costes para la fabricación de cada producto, que supondremos que son constantes e iguales a c. Supondremos, además, que el coste es el mismo para cada una de las empresas. Aquí ya empezamos con problemas puesto que es posible que por motivos técnicos una tenga unos costes de fabricación ligeramente superiores a la otra. De nuevo, al no disponer de información correcta sobre este tema, lo mejor que puedo hacer es intentar no complicarlo más de la cuenta poniendo costes diferentes que, de ocurrir, tampoco serán tan distintos (Siempre podemos al final afinar un poco complicando algo más el modelo).
En cuanto a ingresos, la cosa es algo más peliaguda. Aquí entramos en otra estrategia de diseño en la que la empresa puede incidir, dado que la consola como tal no es un bien que permita satisfacer una necesidad de forma directa, si no a través de los juegos que se compren y jueguen con ella. Esto es, el ingreso potencial de una consola vendida no es únicamente su precio, si no el flujo de beneficios que pueda conseguir extraer de los consumidores que la hayan comprado. Beneficios por juegos first-party, gamepasses, pspluses… Esto permite que en el mercado el precio de las máquinas pueda incluso ser inferior al coste de fabricación, ya que puede expandir mucho más su mercado y recuperar esas perdidas en la venta de otros servicios. PlayStation y Xbox son bienes sustitutivos pero, dentro de cada una de las marcas, los servicios y productos de cada una de ellas son bienes complementarios. Si los juegos de una de las consolas fueran de serie más baratos, por ejemplo si tuviéramos en cuenta el GamePass de Xbox, a lo mejor admitiría que la consola fuera un pelín mas cara, o viceversa.
Por ello, vamos a suponer que los beneficios son iguales a: El precio por consola vendida – los costes por consola vendida + Beneficios potenciales futuros por consola vendida:
Conocemos el diseño de ambas consolas, ciertos elementos técnicos e incluso algunos de los juegos que podremos disfrutar durante estas primeras navidades con olor a generación 4K. Pero no sabemos el precio. Lo intuimos. Lo tememos. Nos empieza a doler la cartera. Alguna hucha que otra ya se ha empezado a llenar. Pero la incertidumbre sobre el precio sigue estando presente. Demasiadas variables y demasiado en juego parecen estar forzando a las compañías a retrasar la decisión sobre un número de 3 cifras que conoceremos en los próximos meses.
A todo esto viene el conocido juego del ratón y el gato. Sony está esperando a Microsoft. Y Microsoft está esperando a Sony. Pero, ¿Por qué?
Como muchas cosas en esta vida la explicación es bastante sencilla pero, como economista que soy, me voy a encargar en este artículo de rodearla de palabraría y un modelito matemático que nos permita hacer algo más serio ese “análisis” de por qué es mejor esperar a decidir el precio.
La información es poder. No es difícil entender por tanto que es mejor decidir con información en la mano que sin ella. Conocer el precio que va a poner tu competidor te deja en bandeja el intentar superarle. Y esperar a que tu competidor muestre sus cartas suele ser una estrategia nada desdeñable. Dicho grosso modo, la empresa X está esperando a que la empresa Y diga su precio para poder poner uno más barato (o para no pasarse de largo) e intentar robar una parte del pastel que le sería más difícil conseguir si ambas tuvieran que decidir y decir el precio con los ojos vendados.
Es curioso, no obstante, que el que elija segundo sea el que salga ganando en este duelo, sobre todo cuando casi todo estudiante de economía acaba sus estudios microeconómicos viendo el modelo de Stackelberg, un modelo en donde el que elije primero, obtiene más beneficio. La diferencia, como siempre es importante recalcar, es que los modelos son abstracciones que se nutren de unas hipótesis iniciales. Si estas no se cumplen, el modelo no nos vale para describir la microrealidad que estamos estudiando. En este caso el modelo de Stackelberg se refiere a la competencia empresarial en cantidades de un producto homogéneo. Esto es: Ambas empresas hacen un producto similar que compartirán el mismo precio en un mercado en dónde los consumidores no distinguen entre empresas. En este contexto, la primera empresa que consiga “copar” el mercado se va a llevar el gato al agua.
La realidad es que la competencia entre Sony y Microsoft se parecen a esos modelos iniciales como un huevo a una castaña. La diferencia fundamental es que ambas empresas están diferenciadas, en mayor o menor grado, y eso implica que aunque exista una cierta sustituibilidad entre los productos que vendan una y otra, no son exactamente iguales. Esa diferenciación implica que cada empresa debe elegir un precio y dejar que los consumidores decidan en base a ese precio cuantas unidades específicas de los productos de esa empresa comprar.
¿Cómo podemos crear un modelo que recoja esta competencia oligopolística (entre dos empresas) con un producto diferenciado que va a competir en precios? Como todo modelo, nos vamos a dejar muchas cosas por el camino, pero intentaremos destacar lo más importante.
Primero, vamos a utilizar unas funciones de demanda con las que he trabajado bastante que son las de Dixit-Stiglitz. Éstas se basan en el concepto de “competencia monopolística”, en donde se intenta unir el hecho de que empresas diferentes con marcas específicas (y por tanto con el monopolio de la identidad de su producto) compiten por satisfacer necesidades concretas o similares (con cierto grado de sustituibilidad entre los productos).
Supondremos que existen dos empresas (empresa 1 y empresa 2). La cantidad de demanda (q) de cada una de las empresas se puede describir de la siguiente manera:
$\begin{equation}
q_{1}=\frac{P_{1}^{-\sigma} \cdot \mu \cdot Y}{P_{1}^{1-\sigma}+P_{2}^{1-\sigma}} \\
q_{2}=\frac{P_{2}^{-\sigma} \cdot \mu \cdot Y}{P_{1}^{1-\sigma}+P_{2}^{1-\sigma}}
\end{equation}$
Lo primero que voy a quitarme de en medio para hacer un poco más simple el análisis es el valor de sigma. Este parámetro mide precisamente el grado de diferenciación del producto. Va desde 1 hasta infinito. Es el valor de la elasticidad de demanda o del grado de homogeneidad del producto.
Si el valor fuera muy alto, significaría que el producto es muy elástico y homogéneo, es decir, un consumidor que tenga que elegir entre las dos empresas elegirá siempre el producto más barato porque, por lo demás, le parecen idénticos.
Si el valor fuera muy bajo, el producto sería menos elástico y, por tanto, más diferenciado. En este caso que una empresa suba el precio va a hacerle perder clientes, pero no muchos, porque tiene una gran parte del mercado que “va a caer al pozo” y comprar su producto siempre y cuando el precio no se vaya de madre. Su producto es tan diferenciado que el que tu producto pueda ser más caro no va a hacer directamente que los clientes salten a comprar los productos de la competencia.
Por descontado, las empresas no solo eligen cuánto producir y a qué precio poner sus productos en las tiendas. La variable de la diferenciación es crucial para crear ese mercado menos elástico sobre el que poder poner unos precios más altos. En el tema que nos toca, las videoconsolas, dos claros ejemplos me vienen a la mente: La potencia y los exclusivos. Pueden diferenciarse intentando meterle más teraflops (la variable de moda en esta entrada a la nueva generación) y además Sony y Microsoft disponen de estudios propios y externos que hacen juegos específicos para sus consolas. En este contexto, comprar la más barata ya no es lo más importante, si lo que quieres es jugar a Bloodborne 2 o al nuevo Halo.
En lo que concierne al modelo, vamos a suponer para hacer las cuentas más simples que el valor es de 2. De esta forma los exponentes quedan más sencillos (después relajaré un poco este supuesto para que podamos ver algunas extensiones interesantes). En cualquier caso, por si a alguno le interesa, la conclusión más importante del parámetro $\sigma$ es que, contra más bajo sea, mayor poder monopolístico tendrán las empresas (más importante será el concepto de marca) y mayor serán los precios y los beneficios. Hasta Desatranques Jaen conoce bien el poder de la diferenciación del producto.
La otra parte que nos queda ($\mu \cdot Y$) hace referencia al dinero que la gente se va a gastar en videoconsolas. Contra mayor sea la renta de la gente($Y$), o mayor sea el % de su gasto que quieran destinar a gastar en videoconsolas ($\mu$, que como es un “bien de lujo” crecerá también conforme crezca la renta), más consolas venderán. Algo bastante obvio que luego realmente no va afectar al precio óptimo.
Vale. ¿Qué hace una empresa para optimizar su producto? Coge su función de beneficio y la optimiza. Si el producto es homogéneo, el precio va a venir determinado por un mercado al que el producto de cada empresa le es indiferente, y lo que la empresa puede decidir es cuánta cantidad quiere producir y enviar al mercado. Si es diferenciado, como en este caso, la empresa tiene un cierto poder de decisión sobre su precio, permitiéndose poner un precio particular a su producto. Supondremos, pues es el origen del análisis de este artículo, que la empresa elije el precio que maximiza su beneficio.
¿Cuál es su beneficio?
Pues ingresos menos costes, claro. Ah, pero para el carro que la cosa no es tan simple. Obviamente la empresa incurrirá en unos costes para la fabricación de cada producto, que supondremos que son constantes e iguales a c. Supondremos, además, que el coste es el mismo para cada una de las empresas. Aquí ya empezamos con problemas puesto que es posible que por motivos técnicos una tenga unos costes de fabricación ligeramente superiores a la otra. De nuevo, al no disponer de información correcta sobre este tema, lo mejor que puedo hacer es intentar no complicarlo más de la cuenta poniendo costes diferentes que, de ocurrir, tampoco serán tan distintos (Siempre podemos al final afinar un poco complicando algo más el modelo).
En cuanto a ingresos, la cosa es algo más peliaguda. Aquí entramos en otra estrategia de diseño en la que la empresa puede incidir, dado que la consola como tal no es un bien que permita satisfacer una necesidad de forma directa, si no a través de los juegos que se compren y jueguen con ella. Esto es, el ingreso potencial de una consola vendida no es únicamente su precio, si no el flujo de beneficios que pueda conseguir extraer de los consumidores que la hayan comprado. Beneficios por juegos first-party, gamepasses, pspluses… Esto permite que en el mercado el precio de las máquinas pueda incluso ser inferior al coste de fabricación, ya que puede expandir mucho más su mercado y recuperar esas perdidas en la venta de otros servicios. PlayStation y Xbox son bienes sustitutivos pero, dentro de cada una de las marcas, los servicios y productos de cada una de ellas son bienes complementarios. Si los juegos de una de las consolas fueran de serie más baratos, por ejemplo si tuviéramos en cuenta el GamePass de Xbox, a lo mejor admitiría que la consola fuera un pelín mas cara, o viceversa.
Por ello, vamos a suponer que los beneficios son iguales a: El precio por consola vendida – los costes por consola vendida + Beneficios potenciales futuros por consola vendida:
$\begin{equation}
B_{1}=P_{1} \cdot q_{1}-c \cdot q_{1}+BP \cdot q_{1}=P_{1} \cdot q_{1}-cn \cdot q_{1} \\
B_{2}=P_{2} \cdot q_{2}-c \cdot q_{2}+BP \cdot q_{2}=P_{2} \cdot q_{2}-cn \cdot q_{2}
\end{equation}$
Donde $cn=c-BP$
Pues ya está. Determinada la función, buscamos el precio óptimo. En un sentido matemático lo que tenemos que hacer es buscar el punto de máximo beneficio que se consigue derivando e igualando a 0 dicha derivada (y luego comprobando que efectivamente se trata de un máximo).
Si hacemos esto para la empresa 2 obtendremos lo siguiente:
Pues ya está. Determinada la función, buscamos el precio óptimo. En un sentido matemático lo que tenemos que hacer es buscar el punto de máximo beneficio que se consigue derivando e igualando a 0 dicha derivada (y luego comprobando que efectivamente se trata de un máximo).
Si hacemos esto para la empresa 2 obtendremos lo siguiente:
$\begin{equation}
P_{2}=cn+\sqrt{cn^2+cn \cdot P_{1}}
\end{equation}$
Lo primero que haremos es suponer que $cn$ es positivo: Los costes de producción son mayores que los posibles beneficios futuros derivados de los servicios extra. Si esto no fuera así, lo mejor sería vender la consola gratis en las puertas de los colegios (o de las oficinas) y esperar pacientemente a que con el paso del tiempo las carteras echen humo. Es básicamente la estrategia de los juegos free to play (fortnite, por poner un ejemplo), o sea que no es imposible en un sentido económico para ciertos productos, pero no creo que sea el caso para una consola (además de que aquí entra en juego otros conceptos como que vender una consola a un precio demasiado bajo podría incluso dar la idea de que es peor de lo que es, y tampoco creo que quieran eso).
La idea con la que vamos a seguir es que hay una empresa que elegirá primero el precio, y una segunda que elegirá después su precio. Supondremos que la que elige segunda es la 2º empresa. Como vemos, en la función de precio óptimo, este depende del precio que haya elegido la primera empresa. Contra más alto sea el precio que haya escogido la primera empresa, más alto se podrá permitir la segunda empresa poner el suyo (la relación entre ambas variables es positiva).
Ahora bien, la empresa que elige primero sabe esto. La primera que salga al escenario (bueno, este año sin E3 ya la primera que haga un video y lo cuelgue en youtube un martes a las 12 de la noche) es consciente de que a los pocos días aparecerá la otra por detrás de la esquina y dará un golpecico en la mesa con su precio. Como lo sabe, lo tendrá en cuenta. Y en el modelo esto implica que a la hora de optimizar su beneficio, la primera empresa usará la función de precio óptimo que va a utilizar la segunda. Las ecuaciones no son más que un registro de la información de la que dispone cada empresa, y en este sentido la primera sabe que con su precio está, en cierto modo, afectando al precio que vaya a sacar la otra empresa, y puede utilizar esto un poco a su favor. Por ejemplo, si Xbox se adelanta y dice que el precio de su consola es de 200 euros (cosa que no va a pasar) estará forzando a Sony a bajar el precio de la suya, y eso Microsoft lo sabe y lo puede utilizar en su favor para intentar “protegerse” de lo que sabe que va a hacer su competidora.
Por eso en microeconomía (o en teoría de juegos) los modelos se hacen un poco más complejos con forme el uso de la información se hace cada vez más compleja (pero es precisamente la gracia, empezar con modelos sencillos y poco realistas e irlos acercando a la realidad poco a poco).
Conociendo todo esto, sustituyendo el precio que pondrá la segunda empresa utilizando la función antes obtenida, el precio óptimo de la empresa que anuncie primero cuánto nos costará saltar de generación es el siguiente:
La idea con la que vamos a seguir es que hay una empresa que elegirá primero el precio, y una segunda que elegirá después su precio. Supondremos que la que elige segunda es la 2º empresa. Como vemos, en la función de precio óptimo, este depende del precio que haya elegido la primera empresa. Contra más alto sea el precio que haya escogido la primera empresa, más alto se podrá permitir la segunda empresa poner el suyo (la relación entre ambas variables es positiva).
Ahora bien, la empresa que elige primero sabe esto. La primera que salga al escenario (bueno, este año sin E3 ya la primera que haga un video y lo cuelgue en youtube un martes a las 12 de la noche) es consciente de que a los pocos días aparecerá la otra por detrás de la esquina y dará un golpecico en la mesa con su precio. Como lo sabe, lo tendrá en cuenta. Y en el modelo esto implica que a la hora de optimizar su beneficio, la primera empresa usará la función de precio óptimo que va a utilizar la segunda. Las ecuaciones no son más que un registro de la información de la que dispone cada empresa, y en este sentido la primera sabe que con su precio está, en cierto modo, afectando al precio que vaya a sacar la otra empresa, y puede utilizar esto un poco a su favor. Por ejemplo, si Xbox se adelanta y dice que el precio de su consola es de 200 euros (cosa que no va a pasar) estará forzando a Sony a bajar el precio de la suya, y eso Microsoft lo sabe y lo puede utilizar en su favor para intentar “protegerse” de lo que sabe que va a hacer su competidora.
Por eso en microeconomía (o en teoría de juegos) los modelos se hacen un poco más complejos con forme el uso de la información se hace cada vez más compleja (pero es precisamente la gracia, empezar con modelos sencillos y poco realistas e irlos acercando a la realidad poco a poco).
Conociendo todo esto, sustituyendo el precio que pondrá la segunda empresa utilizando la función antes obtenida, el precio óptimo de la empresa que anuncie primero cuánto nos costará saltar de generación es el siguiente:
$\begin{equation}
P_{1}=c \cdot \frac{1}{2} \cdot (3+\sqrt{17})
\end{equation}$
Con ella, podemos ya despejar cuál será el precio de la que anuncie su precio después:
$\begin{equation}
P_{2}= c \cdot ( 1+ \sqrt{\frac{1}{2} (5+\sqrt{17} )} )
\end{equation}$
Los números que aparecen son característicos de las simplificaciones que hemos hecho desde el principio y serían más generales (teóricos) si, por ejemplo, hubiéramos dejado la elasticidad como una variable desconocida.
En cualquier caso, una vez conocidas las funciones, podemos comparar ambos precios. Y en este caso nos sale un resultado bastante claro: $\frac{P_{2}}{P_{1}}=0.88$, esto es, la segunda empresa pondrá un precio un 12% inferior a la primera. Si nos movemos en el entorno de un precio de entre 400 y 600 euros, esto implicaría que la segunda empresa debería aprovecharse de anunciar su precio después rebajándolo entre 50 y 70 euros.
Desconocemos (yo al menos) los costes de producción y los beneficios futuros que tienen en cuenta para poder amortizar parte de esos costes, así que no podemos realmente adivinar el precio que Sony o Microsoft, que sí tienen dichos datos, elegirán.
¿Ocurrirá realmente esa diferencia de precios?
No lo creo. Hay muchas más variables en juego: Las consolas no son exactamente igual de potentes, por lo que los costes no tienen por qué ser iguales. Los “beneficios potenciales” que mide cada empresa pueden ser diferentes (según el horizonte temporal o las estrategias que quiera seguir cada una). Vamos a relajar un poco esa consideración inicial de que los costes (o costes netos) eran iguales). Si lo hacemos la resolución del modelo es algo más compleja, pero es la puedo resumir en el siguiente gráfico:
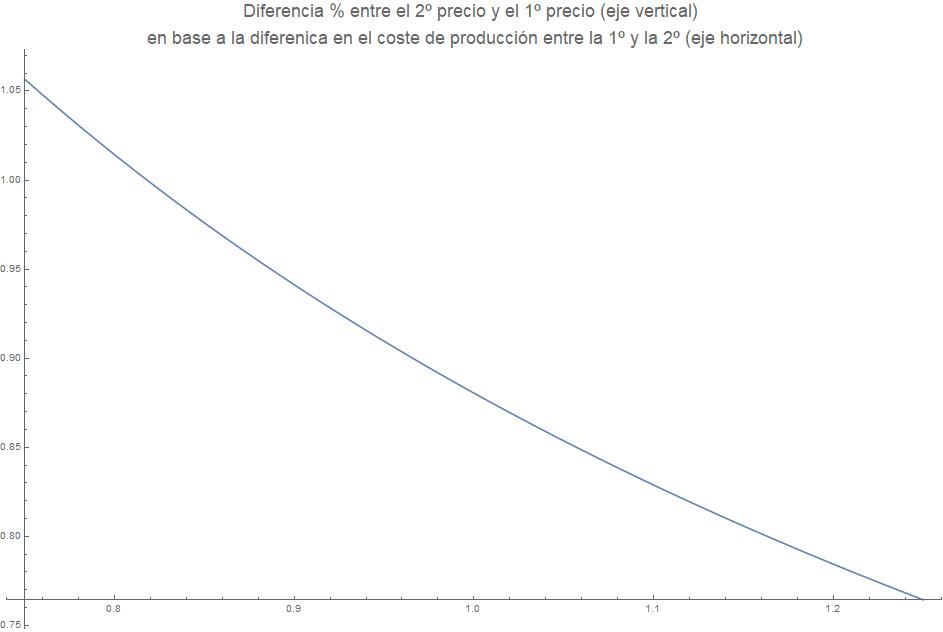
Lo que vemos aquí es en el eje horizontal la proporción de los costes netos de la empresa que elije primero respecto de la empresa que elije en segundo lugar. Por ejemplo, un valor de 0.8 en el eje horizontal implica que la que elije primero tiene una consola con un coste un 20% menor que la segunda consola. Un valor de 1.2 tendría un 20% más en su coste.
En el eje vertical vemos como repercute eso en la diferencia porcentual en el precio de la 2º empresa sobre la primera. Si los costes son iguales (valor en el eje horizontal de 1), la 2º empresa sacará su consola un 12% (lo mismo que hemos obtenido antes, por construcción). Ahora bien, vemos que si la 1º consola es más costosa de producir, la 2º se aprovechará con una mejora relativa en su precio mucho mayor. En cambio, si la primera consola fuera más barata de producir, el precio de las dos sería prácticamente similar.
Podemos también relajar la hipótesis de que la elasticidad sea igual a 2. Si la elasticidad fuera más pequeña, la segunda empresa tendría tanto poder de monopolio (imaginad que toda la población es team-sony o team-xbox y tienen ya decidido cual comprar de antemano independientemente del precio) que podría poner un precio incluso mayor. A su vez, si la elasticidad fuera altísima, con bajar un poco el precio respecto a su competidor ya conseguiría atraer toda su demanda. Tenemos esta curva bastante bonita y no lineal que nos indica que la variabilidad de los posibles precios cambia bastante en base a esta elasticidad. Aunque la diferencia no parece ser mayor del 30% incluso en condiciones ideales.
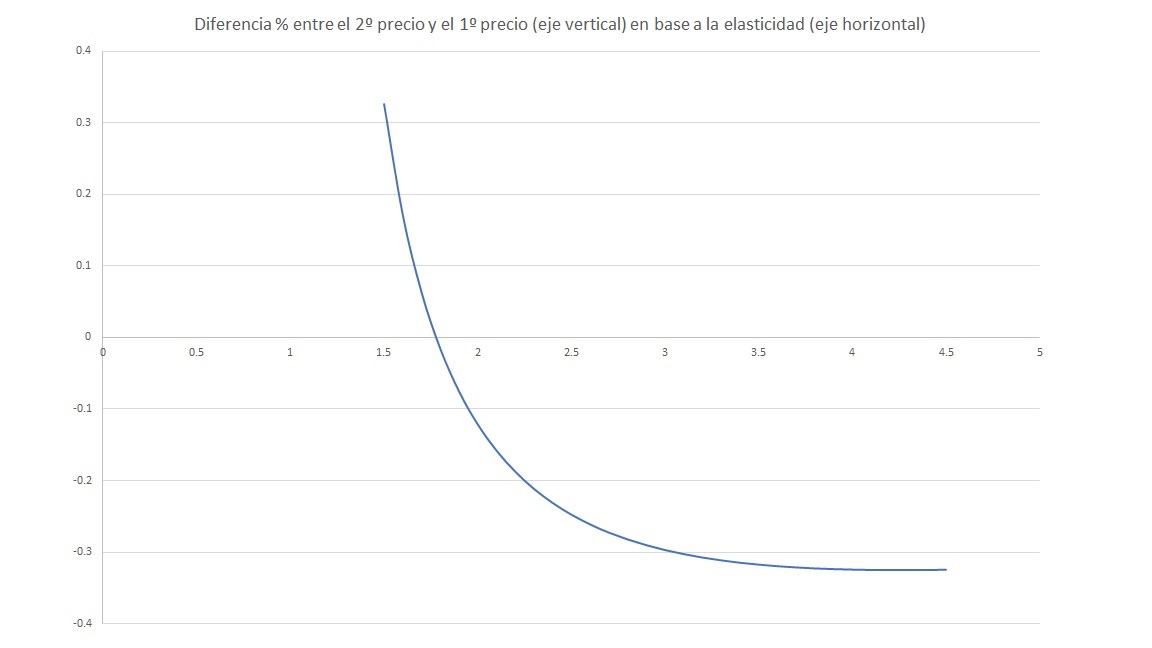
Por suerte, según este estudio parece que la elasticidad en el primer año de la generación es de 1.92, por lo que usar el valor de 2 no es tan descabellado como podría parecer. Diferentes estudios parecen arrojar diferentes datos (3 es otro valor que he visto por ahí), aunque creo que la elasticidad precio es posible que haya ido bajando con el tiempo (al hacerse el ocio videojueguil algo más estable y popular somos menos sensibles a que el precio nos deje sin catar las nuevas experiencias jugables). Con esto en mente, y suponiendo que la elasticidad no será menor que 2, la diferencia puede estar entre un 12% y algo más de un 30%. Si la elasticidad fuera muy alta y la primera consola saliera por 500 euros, la 2º podría llegar a salir por 350 euros. Pero creo que eso es poco realista. Yo personalmente me creo más ese 12%-15% de potencial diferencia.
Otros factores que pueden afectar a la diferencia de precios real: Periféricos que acompañen a la consola, las dos versiones (con lector de discos y solo digital) que pueden empañar el “precio único” de cada consola, lo fuerte o débil que pueda ser la primera tanda de juegos que la acompañen (packs navideños…). Vamos, que no voy a poder adivinar el futuro.
Pero me voy a mojar, qué narices.
Voy a suponer que la Xbox es algo más cara de producir. Quizá me equivoque, pero viendo que tiene algo más de teraflops y que su disco duro SSD es posible que sea más grande, voy a tirar con esa hipótesis. Con esto en mente:
Si Sony presenta primero su precio y Xbox después: Los precios serán similares. Si tuviera que apostar algo más, diría 500 euros cada una.
Si Xbox lo anuncia primero y Sony después, la PS5 será 60 euros más barata. Si tuviera que apostar algo más, diría 550 euros la Xbox y 490 la Ps5.
Así que con eso me quedo, en un par de meses la realidad caerá sobre este artículo como un mazo, echando por tierra cualquier atisbo de certera adivinación. Pero al menos ha sido divertido.
En cualquier caso, una vez conocidas las funciones, podemos comparar ambos precios. Y en este caso nos sale un resultado bastante claro: $\frac{P_{2}}{P_{1}}=0.88$, esto es, la segunda empresa pondrá un precio un 12% inferior a la primera. Si nos movemos en el entorno de un precio de entre 400 y 600 euros, esto implicaría que la segunda empresa debería aprovecharse de anunciar su precio después rebajándolo entre 50 y 70 euros.
Desconocemos (yo al menos) los costes de producción y los beneficios futuros que tienen en cuenta para poder amortizar parte de esos costes, así que no podemos realmente adivinar el precio que Sony o Microsoft, que sí tienen dichos datos, elegirán.
¿Ocurrirá realmente esa diferencia de precios?
No lo creo. Hay muchas más variables en juego: Las consolas no son exactamente igual de potentes, por lo que los costes no tienen por qué ser iguales. Los “beneficios potenciales” que mide cada empresa pueden ser diferentes (según el horizonte temporal o las estrategias que quiera seguir cada una). Vamos a relajar un poco esa consideración inicial de que los costes (o costes netos) eran iguales). Si lo hacemos la resolución del modelo es algo más compleja, pero es la puedo resumir en el siguiente gráfico:

Lo que vemos aquí es en el eje horizontal la proporción de los costes netos de la empresa que elije primero respecto de la empresa que elije en segundo lugar. Por ejemplo, un valor de 0.8 en el eje horizontal implica que la que elije primero tiene una consola con un coste un 20% menor que la segunda consola. Un valor de 1.2 tendría un 20% más en su coste.
En el eje vertical vemos como repercute eso en la diferencia porcentual en el precio de la 2º empresa sobre la primera. Si los costes son iguales (valor en el eje horizontal de 1), la 2º empresa sacará su consola un 12% (lo mismo que hemos obtenido antes, por construcción). Ahora bien, vemos que si la 1º consola es más costosa de producir, la 2º se aprovechará con una mejora relativa en su precio mucho mayor. En cambio, si la primera consola fuera más barata de producir, el precio de las dos sería prácticamente similar.
Podemos también relajar la hipótesis de que la elasticidad sea igual a 2. Si la elasticidad fuera más pequeña, la segunda empresa tendría tanto poder de monopolio (imaginad que toda la población es team-sony o team-xbox y tienen ya decidido cual comprar de antemano independientemente del precio) que podría poner un precio incluso mayor. A su vez, si la elasticidad fuera altísima, con bajar un poco el precio respecto a su competidor ya conseguiría atraer toda su demanda. Tenemos esta curva bastante bonita y no lineal que nos indica que la variabilidad de los posibles precios cambia bastante en base a esta elasticidad. Aunque la diferencia no parece ser mayor del 30% incluso en condiciones ideales.

Por suerte, según este estudio parece que la elasticidad en el primer año de la generación es de 1.92, por lo que usar el valor de 2 no es tan descabellado como podría parecer. Diferentes estudios parecen arrojar diferentes datos (3 es otro valor que he visto por ahí), aunque creo que la elasticidad precio es posible que haya ido bajando con el tiempo (al hacerse el ocio videojueguil algo más estable y popular somos menos sensibles a que el precio nos deje sin catar las nuevas experiencias jugables). Con esto en mente, y suponiendo que la elasticidad no será menor que 2, la diferencia puede estar entre un 12% y algo más de un 30%. Si la elasticidad fuera muy alta y la primera consola saliera por 500 euros, la 2º podría llegar a salir por 350 euros. Pero creo que eso es poco realista. Yo personalmente me creo más ese 12%-15% de potencial diferencia.
Otros factores que pueden afectar a la diferencia de precios real: Periféricos que acompañen a la consola, las dos versiones (con lector de discos y solo digital) que pueden empañar el “precio único” de cada consola, lo fuerte o débil que pueda ser la primera tanda de juegos que la acompañen (packs navideños…). Vamos, que no voy a poder adivinar el futuro.
Pero me voy a mojar, qué narices.
Voy a suponer que la Xbox es algo más cara de producir. Quizá me equivoque, pero viendo que tiene algo más de teraflops y que su disco duro SSD es posible que sea más grande, voy a tirar con esa hipótesis. Con esto en mente:
Si Sony presenta primero su precio y Xbox después: Los precios serán similares. Si tuviera que apostar algo más, diría 500 euros cada una.
Si Xbox lo anuncia primero y Sony después, la PS5 será 60 euros más barata. Si tuviera que apostar algo más, diría 550 euros la Xbox y 490 la Ps5.
Así que con eso me quedo, en un par de meses la realidad caerá sobre este artículo como un mazo, echando por tierra cualquier atisbo de certera adivinación. Pero al menos ha sido divertido.